
Tata Institute of Fundamental Research
Colorful Extensions of Infinite (p,q)-Theorems in Combinatorial Geometry
STCS Seminar
Speaker:
Arijit Ghosh (Indian Statistical Institute)
Organiser:
Arkadev Chattopadhyay
Date:
Tuesday, 27 Aug 2024, 16:00 to 17:00
Venue:
A-201 (STCS Seminar Room)

(Scan to add to calendar)
Abstract:
An infinite sequence of sets  is said to be a heterochromatic sequence for an infinite collection
is said to be a heterochromatic sequence for an infinite collection  of families of sets, if there exists a strictly increasing sequence of natural numbers
of families of sets, if there exists a strictly increasing sequence of natural numbers  such that for all
such that for all  we have
we have  . In this talk, we will prove that if for each
. In this talk, we will prove that if for each  is a family of nicely shaped convex sets in
is a family of nicely shaped convex sets in  such that each heterochromatic sequence
such that each heterochromatic sequence  of
of  contains
contains  sets that can be pierced by a single
sets that can be pierced by a single 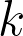 -flat (
-flat ( 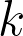 -dimensional affine space) then all but finitely many
-dimensional affine space) then all but finitely many  's can be pierced by finitely many
's can be pierced by finitely many 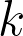 -flats. This result generalizes the
-flats. This result generalizes the ) -Theorem proved by Keller and Perles (SoCG'22) to the countably colorful setting. We have also established the tightness of our results by proving several no-go theorems.
This is a joint work with Sutanoya Chakraborty (PhD Student at ISI, Kolkata) and Soumi Nandi (PhD Student at ISI, Kolkata).
-Theorem proved by Keller and Perles (SoCG'22) to the countably colorful setting. We have also established the tightness of our results by proving several no-go theorems.
This is a joint work with Sutanoya Chakraborty (PhD Student at ISI, Kolkata) and Soumi Nandi (PhD Student at ISI, Kolkata).
Short Bio:
Arijit Ghosh is currently an Associate Professor at ACM Unit, Indian Statistical Institute, Kolkata. He did his PhD in Computer Science from INRIA, France, and was a Postdoc at Max Planck Insitute for Informatics, Germany.
| Speaker: | Arijit Ghosh (Indian Statistical Institute) |
| Organiser: | Arkadev Chattopadhyay |
| Date: | Tuesday, 27 Aug 2024, 16:00 to 17:00 |
| Venue: | A-201 (STCS Seminar Room) |
(Scan to add to calendar)
Abstract:
An infinite sequence of sets  is said to be a heterochromatic sequence for an infinite collection
is said to be a heterochromatic sequence for an infinite collection  of families of sets, if there exists a strictly increasing sequence of natural numbers
of families of sets, if there exists a strictly increasing sequence of natural numbers  such that for all
such that for all  we have
we have  . In this talk, we will prove that if for each
. In this talk, we will prove that if for each  is a family of nicely shaped convex sets in
is a family of nicely shaped convex sets in  such that each heterochromatic sequence
such that each heterochromatic sequence  of
of  contains
contains  sets that can be pierced by a single
sets that can be pierced by a single 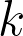 -flat (
-flat ( 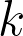 -dimensional affine space) then all but finitely many
-dimensional affine space) then all but finitely many  's can be pierced by finitely many
's can be pierced by finitely many 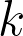 -flats. This result generalizes the
-flats. This result generalizes the ) -Theorem proved by Keller and Perles (SoCG'22) to the countably colorful setting. We have also established the tightness of our results by proving several no-go theorems.
-Theorem proved by Keller and Perles (SoCG'22) to the countably colorful setting. We have also established the tightness of our results by proving several no-go theorems.
This is a joint work with Sutanoya Chakraborty (PhD Student at ISI, Kolkata) and Soumi Nandi (PhD Student at ISI, Kolkata).
Short Bio:
Arijit Ghosh is currently an Associate Professor at ACM Unit, Indian Statistical Institute, Kolkata. He did his PhD in Computer Science from INRIA, France, and was a Postdoc at Max Planck Insitute for Informatics, Germany.